alpyrithm_알파이리즘
[알고리즘][Python] 백준(BOJ) 1920 수 찾기_파이썬 본문
1-1. 탐색과 정렬 (1)
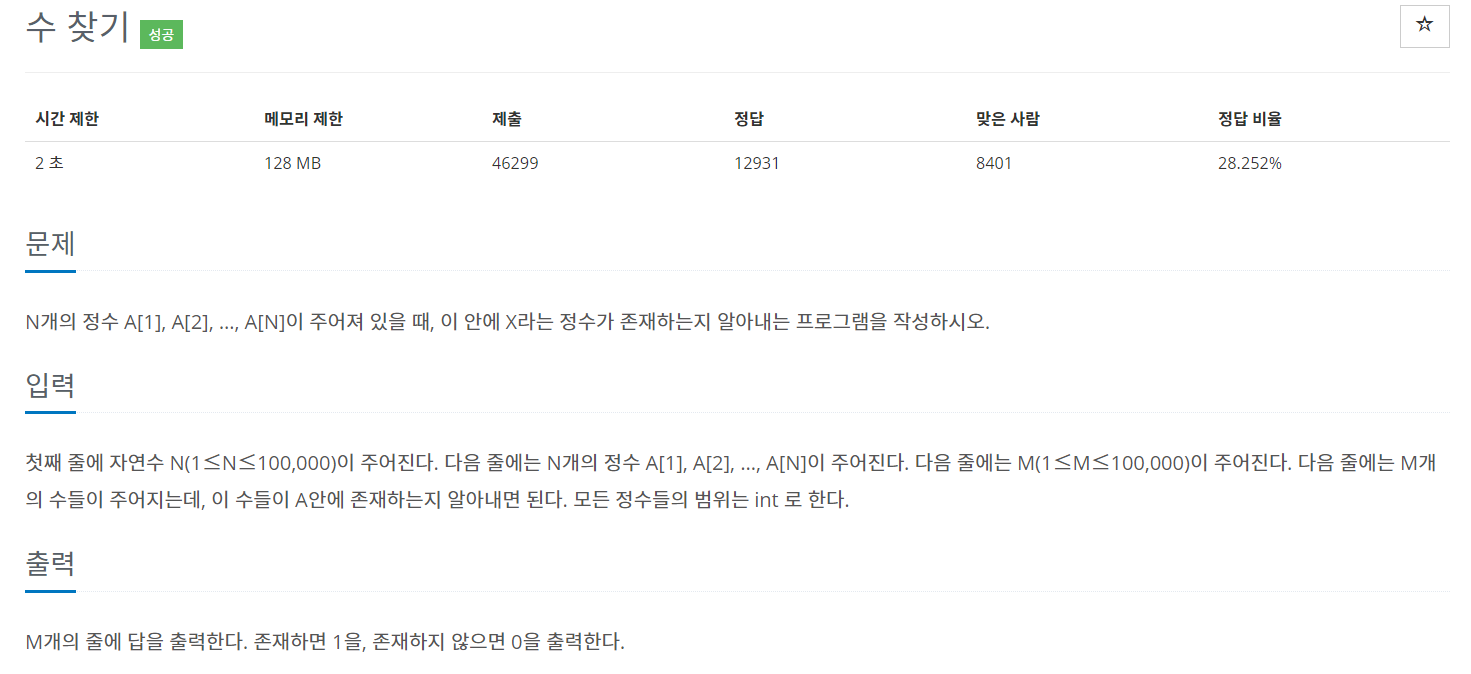
A - 1920 수 찾기 https://www.acmicpc.net/problem/1920
1920번: 수 찾기
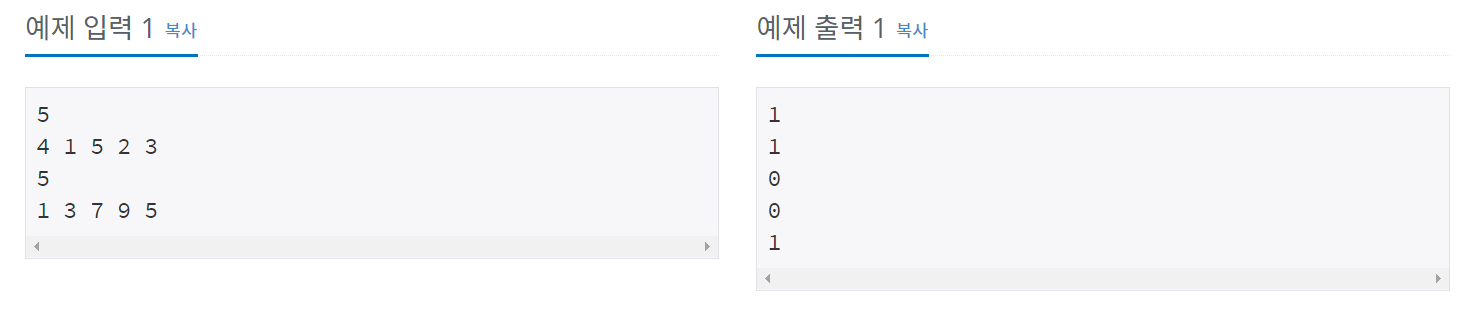
첫째 줄에 자연수 N(1≤N≤100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1≤M≤100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들이 A안에 존재하는지 알아내면 된다. 모든 정수들의 범위는 int 로 한다.
www.acmicpc.net
문제 풀기 전 공부할 것 : 이진 탐색, 정렬
풀이 1
이진 탐색은 값을 비교할 때마다 찾는 값이 있을 범위를 절반씩 좁히면서 탐색하는 효율적인 탐색 알고리즘이다.
이진 탐색의 계산 복잡도는 O(logn)으로 순차 탐색보다 더 효율적이다.
이진 탐색을 하기 위해서는 반드시 자료를 미리 정렬해야 한다.
import sys
def binary_search(a, x):
start = 0
end = len(a) - 1
while start <= end:
mid = (start + end) // 2
if x == a[mid]:
return 1
elif x > a[mid]:
start = mid + 1
else:
end = mid - 1
return 0
n = int(input())
a = list(map(int, sys.stdin.readline().split()))
a.sort() # 리스트 정렬
m = int(input())
x = list(map(int, sys.stdin.readline().split()))
for k in range(m):
print(binary_search(a, x[k]))+) input()보다 sys.stdin.readline()이 빠르다 => 시간을 단축시킬 수 있다
+) 정렬에는 sort()와 sorted()가 있다.
풀이 2
이진 탐색을 재귀 호출로 풀 수 있다.
def binary_search(a, x, start, end):
if start > end:
return False
mid = (start + end) // 2
if a[mid] == x:
return True
elif a[mid] > x:
return binary_search(a, x, start, mid-1)
else:
return binary_search(a, x, mid+1, end)
n = int(input())
a = list(map(int, input().split()))
m = int(input())
m_l = list(map(int, input().split()))
a = sorted(a) # 리스트 정렬
for m in m_l:
if binary_search(a, m, 0, n-1):
print(1)
else:
print(0)
풀이 3
python 재귀로 풀 때
import sys
sys.setrecursionlimit(limit)를 추가해줘야 한다.
재귀 함수가 있는 경우 최대 재귀 깊이를 설정해줘야 한다. 파이썬에서 최대 재귀 기본값은 1000 레벨이며 이는 sys 모듈의 setrecursionlimit 기능을 사용하여 변경할 수 있다.
이 문제의 경우 문제없이 돌아가지만 DFS, BFS의 경우 런타임 오류가 뜨는 경우가 있다. 따라서 재귀 허용 깊이를 수동으로 늘려주는 코드를 코드 상단에 적어줘야 한다.
* PyPy에서는 sys.setrecursionlimit(limit)이 작동하지 않음을 유의해야 한다. 즉 임의로 재귀 호출 깊이를 설정할 수 없다.
자료 정렬을 병합 정렬로 정렬하였다.
병합 정렬은 이미 정렬된 두 그룹을 맨 앞에서부터 비교하면서 하나로 합치는 병합 과정으로 정렬하는 알고리즘이다. 주어진 자료를 절반으로 나눈 다음 각각을 재귀 호출로 풀어 가는 방식이다.
따라서 병합 정렬의 계산 복잡도는 O(n·logn)이다.
import sys
sys.setrecursionlimit(100000)
def merge_sort(a):
if len(a) == 1:
return a
elif len(a) == 2:
return arr if a[0] < a[1] else a[::-1]
mid = len(a) // 2
left = merge_sort(a[:mid])
right = merge_sort(a[mid:])
return merge(left, right)
def merge(left, right):
res =[]
while left and right:
if left[0] > right[0]:
res.append(right.pop(0))
else:
res.append(left.pop(0))
return res + (left if left else right)
def binary_search(a, x, start, end):
if start > end:
return 0
mid = (start + end) // 2
if a[mid] == x:
return 1
elif a[mid] > x:
return binary_search(start, mid-1)
else:
return binary_search(mid+1, end)
N = int(input())
a = merge_sort(list(map(int, input().split())))
M = int(input())
for x in list(map(int, input().split())):
print(binary_search(a, x, 0, N-1))
풀이 4
이진 탐색으로 푸는 문제이긴 하나 dictionary(hashtable)를 이용하여 풀 수도 있다.
N = int(input())
a = list(map(int, input().split()))
M = int(input())
m_l = list(map(int, input().split()))
dic = {}
for n in a:
index = n % 10
if index in dic:
dic[index].append(n) # 4, 14가 a에 있다면 dic = {4: [4, 14]}와 같이 표현됨
else:
dic[index] = [n]
for m in m_l:
index = m % 10
found = 0
if index in dic:
for h in dic[index]:
if h == m:
found = 1
print(found)
시도 1 ==> 시간 초과
순차 탐색으로 리스트 a에 있는 모든 수와 비교하여 문제 해결
순차 탐색 알고리즘의 최악의 경우 비교가 최대 n(len(a))번 필요하다.
따라서 계산 복잡도는 O(n)이다.
def search_num(a, x): # 리스트 a 안에 x라는 정수가 존재하는지 알아내는 함수
n = len(a) # 리스트 a의 원소 수
for i in range(n): # 순차 탐색
if a[i] == x:
return 1
return 0
n = int(input())
a = input()
a = list(map(int, a.split()))
m = int(input())
x = input()
x = list(map(int, x.split()))
for k in range(m):
print(search_num(a, x[k]))시도 2 ==> 시간 초과
시도 1의 시간 초과에서 시간을 줄이는 방법을 두 가지 생각해보았다.
1. input() 함수에서 시간 단축
2. 순차 탐색 알고리즘 대신 다른 알고리즘을 사용하는 방법
+ python 대신 pypy로 제출
시도 2에서는 1번의 방법을 먼저 시도하였다.
input() 대신 sys를 import 하여 sys.stdin.readline()을 사용하였고 pypy로 제출했으나 여전히 시간 초과였다.
따라서 순차 탐색이라는 방법에 문제가 있음을 알 수 있다.
import sys
def search_num(a, x): # 리스트 a 안에 x라는 정수가 존재하는지 알아내는 함수
n = len(a) # 리스트 a의 원소 수
for i in range(n): # 순차 탐색
if a[i] == x:
return 1
return 0
n = int(input())
a = list(map(int, sys.stdin.readline().split()))
m = int(input())
x = list(map(int, sys.stdin.readline().split()))
for k in range(m):
print(search_num(a, x[k]))
복습
순차 탐색 알고리즘 vs 이진 탐색 알고리즘
병합 정렬 알고리즘


